На следующих страницах:

Андрей Сафонов. Переписка Лейбница – Кларка

Андрей Сафонов

Павел Флоренский, Георг Кантор
и проблема творчества в математике

Оглавление

Введение…………………………………………………….................С. 3
1. Истина есть антиномия………………………………………….....С. 6
2. Изображение антиномии в теории множеств. “Нигде страна”… C. 9
3. Иррационализм в математике. Земля и небо……………………..С. 10
4. Потенциальная и актуальная бесконечность. От земли к небу….С. 14
5. Мнимости в геометрии: зазеркалье………………………………..С. 19
6. Точка перехода. И еще раз проблема континуума………………...С. 29
Заключение…………………………………………………………….С. 35
Библиографический список……………………………………..........С. 36 

Введение

Наследие священника и ученого Павла Флоренского является крайне интересным для математической философии по очень многим причинам.

Начнем издалека. В «Критике чистого разума» Иммануил Кант выделял две формы познания – аналитическую и синтетическую. Первая расщепляет уже данные человеку понятия на части в соответствии с правилами формальной логики – т.е. фактически не создает ничего нового, делая просто некую развертку уже наличествовавшего, второе является источником самих понятий. То есть именно синтез дает ткань познания, в то время как аналитические операции без него являются фактически игрой со значками. Таким образом, любая наука, чтобы иметь какую-то познавательную ценность, должна апеллировать к синтезу.

Для синтетического знания необходим источник, причем этот источник не может содержаться в соответствии с вышесказанным в правилах функционирования рассудка – нужно что-то помимо логики. Для наук об окружающем мире этот источник Кант вполне естественно видит в чувственном опыте, однако самая точная наука – математика – лишена этого опыта. Кант разрешает эту проблему достаточно красиво: источником синтетического знания в математике, утверждает философ, является встроенная, априорно принадлежащая человеческой душе форма восприятия – пространство.

Кант вслед за Лейбницем отрицал объективность пространства, считая  его свойством души, своего рода фильтром, через который субъект получает информацию об объекте.

Из этого  источником, находящегося “между” познающим и познаваемым и извлекается математика. Созерцание дает аксиомы и понятия – своего рода “material prima” для математики, из которой уже путем аналитических преобразований возводится здание этой науки, содержавшееся  потенциально еще в самом начале – в пространстве как форме созерцания. Примечательно, что Кант говорил о том, что можно создать альтернативные  структуры, взяв аксиомы произвольно. Однако это, как он считал, не представляет никакой познавательной ценности – истинная математика может быть только одна.

“Воды” науки, начали разрушать кантовскую плотину практически сразу после возведения.

Сначала геометрией Лобачевского, выбившей пятый постулат Эвклида, и позволившей проводить через точку, более одной прямой параллельной данной, потом  все более изощренными обобщениями Александрова, Гильберта, Минковского. В современной математике эвклидово пространство является лишь очень частным случаем, продолжая, тем не менее, быть царем человеческого опыта.

Что же произошло? С кантовской точки зрения все неэвклидовы конструкции являются пустой аналитической игрой, т.к. нарушено главное условие получения знания – опора на созерцание. Отказываться от нее стали достаточно осторожно – Лобачевский изменил пятый постулат, который гласит, что через точку не лежащую на прямой можно провести только единственную прямую, ей параллельную, как раз-таки из-за того, что это не является визуально очевидным.  Постепенно математики отказались выводить аксиомы из созерцания и аксиомами стали любые принимаемые без доказательства утверждения, удовлетворяющие трем требованиям:

1) Непротиворечивость – выводы из них не должны противоречить друг-другу;

2) Полнота – любое утверждения в рамках заданной системы должно быть доказанным;

3) Минимальность – невозможность вывести одну аксиому из другой.

Но где теперь искать источник для синтеза?

Конечно, можно подойти к созданиям новых структур чисто механически – принимая за аксиоматики любые утверждения, удовлетворяющие вышеприведенным требованиям. Такой подход использовала группа французских математиков Бурбаки. Однако, несмотря оказанное на последующее развитие науки влияние, он был подвергнут широкой критике со стороны зарубежных и российских ученых. Наиболее ярким противником Бурбаки является создатель теории катастроф В.И. Арнольд, основными обвинениями которого было колоссальное раздувание науки, создание гиперсложных монструозных объектов, убийство духа математики. Интересно, что подход  Бурбаки внедрялся в 70-е годы в систему советского школьного образования. Инициатором этого являлся выдающийся математик Николай Колмогоров. Результаты реформы, согласно многочисленным свидетельствам, оказались катастрофическим. Полная формализация, на основе понятия алгебраической структуры привела к тому, что дети перестали понимать элементарные геометрические теоремы, а у целого поколения сложилось впечатление, что математика является абсолютно оторванной от опыта наукой, занятой формально-логическими перестановками.

В России от реформы в конце концов отказались, однако в Европе наследие Бурбаки обрело более благодатную почву. В результате развития этих идей сложилось представление о математике как о языке, наиболее четко выраженное немецким ученым Ю.И.  Маниным.

Он определяет математику как раздел филологии или лингвистики: это наука о формальных преобразованиях одних наборов символов некоторого конечного алфавита в другие при помощи конечного числа специальных "грамматических правил".

Отличие математики от живых языков состоит, по Манину, лишь в том, что в ней больше грамматических правил. Например, имеется правило, позволяющее заменять символы "1+2" на "3".

Став разделом лингвистики, математика становится жертвой процессов, рассматриваемых посструктуралистами и постмодернистами – как часть языка, она становится замкнутой на себе реальностью, оторванной от остального мира.

Мы опять возвращаемся к предупреждению Канта о занятиях пустой аналитикой – а построение математики только из логических условий, накладываемых на аксиоматику, этим и является.

Для того, чтобы разорвать кольцо, чтобы математика не являлась замкнутой в себе грамматикой, нужен источник синтеза, которым Кант предлагал созерцание. Однако “консервативная революция”, состоящая в отказе от всех “многомерных” конструкций и возврате к “старой доброй” эвклидовой геометрии в качестве единственной, вряд ли возможна и нужна, тем более что неэвклидова математика имеет многочисленные применения в науке и технике.

Мы оказываемся в парадоксальной ситуации, если полностью доверимся “Критике чистого разума”, зажатые между априорностью и необходимостью развивать математику, находящуюся за пределами привычного созерцания. Но именно в этом парадоксальном пространстве, происходит работа духа современной математики, работа интуиции. 

Потенциальная математическая вселенная, заложенная в трех элементарных логических требованиях, является поистине беспредельной - поэтому работа математика становится подобной искусству скульптора. Согласно античным представлениям статуя изначально содержится в камне, задача творца в том, чтобы “открыть” ее, убрав все лишнее. С этой же работой,  кстати, Павел Флоренский сравнивал опыт восстановления православной традиции. Именно здесь проявляется та самая работа духа математики – из хаоса создается космос.

Для иллюстрации приведем отрывок из статьи Марии Луизы фон Франц “ Наука и подсознание”, в котором она цитирует двух великих математиков, рассказывающих о процессе математического творчества:

“Немецкий математик XVIII столетия Карл Фридрих Гаусс описал переживание подобной подсознательной упорядоченности идей. Ему надо было найти одну закономерность в теории чисел, и он обнаружил ее "не в результате упорных исследований, а благодаря, так сказать, милости Божьей. Ответ пришел внезапно сам собой, как молниеносное озарение, и я не мог понять или найти связь между данными, известными мне раньше, с которыми я последний раз экспериментировал, и тем, что породило конечный успех". Французский ученый Анри Пуанкаре еще подробнее описал подобное явление. Однажды бессонной ночью он увидел, как в нем сталкиваются математические образы, идеи, представления. Наконец некоторые из них "соединились более устойчивым образом. Ощущение было такое, будто наблюдаешь непосредственно за работой подсознания, причем его деятельность постепенно начинает частично проявляться в сознании, не теряя собственной природы. В такие моменты интуитивно понимаешь, как могут функционировать два эго".   [15,183]

Как же происходит работа этой загадочной интуиции? С чисто логической точки зрения нам нужен прообраз, что-то вроде платоновских эйдосов или кантовских априорных форм, в соответствии с которым будет вырезаться наша “статуя”. Создание неэвклидовой геометрии заставляет нас предположить существование некой другой, не кантовской, априорности – более динамической, более широкой, менее явной, похожей скорее на пространство коллективного бессознательного, о котором говорил психолог Юнг, оставляя за ним априорность для человеческой психики. Этот подход в математической философии наиболее ярко выражен Шпенглером в известной работе “Закат Европы”.

В главе “О смысле чисел” он называет идею Канта о первичности эвклидового созерцания ошибкой слишком рационального ума. Созерцание по Шпенглеру есть нечто более подвижное, связанное с культурой, к которой принадлежит созерцатель. Математика это функция культуры. Нет универсальной математики – говорил Шпенглер.

У неоплатоников была идея о живой фантазии [7], огненной пневме, сходные идеи находил французский исследователь Анри Корбин  у исламского мистика Сахраварди, говорившем о метафизическом воображении, одинаково трансцендентном действительности и миру грез, позволяющему непосредственно созерцать тайные законы бытия, эту внутреннюю область он называл na-koja-abad –“нигде страной” [16].

Возможно где-то там в огненной пневме, в “нигде стране” происходит конструирование математики.

В этом контексте наследие Павла Флоренского представляется уникальным – в своих трудах он открыто совмещал мистическую религиозную интуицию и математику, без всякого логического ущерба для последней.

Флоренский был сторонником идеи о сведении ума к сердцу, являвшейся ключевой у монахов–исихастов. Согласно этой идее мысль рождается в сердце, мозг же является отражающим звеном, оформляющем ее в привычную нам структуру. Во многих традиционных религиях в связи с этим сердце уподобляется солнцу, а мозг луне.

В таком привычном для антиномичном режиме слияния ума и сердца и движется  мысль философа.

Для рассмотрения работы творческой составляющей в математике нам крайне интересно будет проследить за ее развитием.

1. Истина есть антиномия

Прежде чем перейти к математическим изысканиям философа, необходимо составить представление о парадоксальном стиле его мышления. Философия Павла Флоренского неотделима от православной веры – изощренные логические спекуляции используемые им, являются прежде всего иллюстрацией церковного догмата.

Философ разделял божественную Истину, находящуюся “за двойной гранью пространства и времен”, для которой  “форма и содержание – одно” и истину – знание об истине, доступное твари ниспавшей во время и пространство.

“Несомненно, что наряду с Истиною необходимо существует и истина, если только наряду с Богом существует тварь. Существование истины есть лишь иное выражение самого факта существования твари, как таковой, т. е. как лежащей личным много-образием во времени и общественным — в пространстве. Наличность истины равна наличности твари.” [11,134-135]

Однако для того, чтобы являться истиной знание твари должно находиться в некой связи с Истиной.

“Хотя и в твари данная, однако истина должна быть монограммою Божества. По-сю-сторонняя, она должна быть как бы не по-сю-сторонней. Красками условного она должна обрисовать Безусловное. В хрупком сосуде человеческих слов должен содержаться присно-несокрушимый Адамант божества. Тварь мятется и кружится в бурных порывах Времени; истина же должна пребывать. Тварь рождается и умирает, и поколения сменяются поколениями; истина же должна быть нетленной” [11,136].

Таким образом, истина должна находиться выше всяких условий, “Но как это возможно? Как возможно из условного материала человеческого ума построить безусловную формулу Истины божественной?” [11,136]

Размышляя над этим, философ приходит к парадоксальному выводу, ставшему стержнем его философии – “истина есть антиномия”:

“Рассудочная формула тогда и только тогда может быть превыше нападений жизни, если она всю жизнь вберет в себя, со всем ее много-образием и со всеми ее наличными и имеющими быть противоречиями. Рассудочная формула может быть истиною тогда и только тогда, если она, так сказать, предусматривает все возражения на себя и отвечает на них. Но, чтобы предусмотреть все возражения, — надо взять не их именно конкретно, а предел их. Отсюда следует, что истина есть такое суждение, которое содержит в себе и предел всех отменений его, или, иначе, истина есть суждение само-противоречивое”. [11,137]

Термин “антиномия” введен в философию Кантом в “Критике чистого разума”, однако идея о самопротиворечивости рассудка беспокоила философов достаточно давно – начиная с Гераклита, утверждавшего, что из противоположностей рождается гармония. Средневековый богослов Николай Кузанский видел истину, как “высочайшее единство всех противоположностей”. Идея единства и борьбы противоположностей является ключевой  в гегелевской диалектике. Однако в чем же уникальность использования антиномии у Павла Флоренского? Если у Канта антиномии играли роль печальных указателей пределов человеческого познания, невозможности рассудка дать ответы на главные вопросы, то для Флоренского они являются вестью об  Истине, спасительными огнями, ведущими прочь от “эгоистического самоудовлетворения рассудка”. Высказывания антиномии является подвигом, актом самоотречения .

Мысль философа движется между да и нет,  являясь “интуитивной дискурсией” и “дискурсивной интуицией”, в ней мы отчетливо наблюдаем  то самое соединение сердца и разума о котором говорилось во введении.

К вопросу противоречивости математика подошла вплотную в начале двадцатого века, решение его стало “осознанной необходимостью”. Его формулирует Гильберт в 1900 году, как вторую из своих проблем, определивших развитие математики как минимум на последующие сто лет. Проблема звучит так: аксиомы арифметики противоречивы или нет?

В 1930 году Гедель ответил на этот вопрос своими теоремами о неполноте.

Первая теорема утверждает, что если формальная арифметика непротиворечива, то в ней существует невыводимая и неопровержимая формула.

Фактически теорема Геделя говорит о существовании своего рода “сингулярных” точек в математике, в которых нарушаются  условия, накладываемые на математическую теорию.

Значимость этого открытия трудно переоценить. Согласно ему даже самая точная наука математика, неспособна избежать изначальной расколотости рассудка, она никогда не станет полной и непротиворечивой, т.е. истинной  в смысле христианского богословия.

Попытка завершить здание любой формальной теории приводит к ее обрушению.

Это полностью резонирует со следующими рассуждениями Павла Флоренского:

“ Рассудочные операции ведут к таким комбинациям, которым нет уже места в среде своих производителей и которые требуют разрыва рассудочной области, чтобы родиться в новый, дотоле невиданный и немыслимый мир. ” [11,397]

Таким образом, теорема Геделя является логическим выражением расколотости рассудка, о которой говорил Флоренский, но она же является   двигателем математики, как у Гегеля - противоречия двигают познающий дух. Невозможность замкнуть рассудочную петлю приводит к новому витку развития. Именно здесь происходит загадочная работа сверхрассудочного синтеза.

2. Изображение антиномии в теории множеств.

“Нигде страна”

Любой логической операции можно найти соответствие в теории множеств. Это дает интересную возможность “созерцать” работу рассудка. Рассмотрим изображение антиномии. Итак, у нас есть два противоположных утверждения, им будут соответствовать два взаимодополняющих множества, покрывающих все пространство.

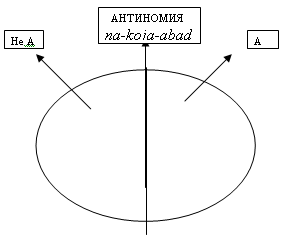
Антиномия предполагает одновременное выполнение А и не А, то есть, на нашем рисунке для нее не существует соответствия,  она не созерцаема,  можно сказать, что она находится “нигде”.

Это похоже на уже упомянутую, na-koja-abad –“нигде страну”  исламского мистицизма, находящеюся по ту сторону чувственного, в которой возможно непосредственное созерцание метафизических принципов.

В дальнейшем мы увидим уместность подобного сравнения, применительно к нашему исследованию.

3. Иррационализм в математике. Земля и небо

Павел Флоренский говорил о подвиге рассудка как об опыте самопреодоления, рассудок должен принести себя в жертву, чтобы открылась его сверхлогическая основа:

“В самом деле: рассудок, в своих конститутивных логических нормах, и л и  насквозь нелеп, безумен до тончайшей своей структуры, сложен из элементов бездоказательных и потому вполне случайных,  и л и   же он имеет своею основою сверх-логическое. Что-нибудь одно:  и л и  нужно принять принципиальную случайность законов логики,  и л и   же неизбежно признание сверх-логической основы этих норм, – основы, с точки зрения самого рассудка, постулативно-необходимой, но тем самым имеющей  д л я   р а с с у д к а   антиномический закал. И то и другое выводит  з а   пределы рассудка. Но первое разлагает рассудок, внося в сознание вечно-безумную  агонию, а  второе укрепляет его подвигом само-преодоления, – крестом, который есть для рассудка нелепое отторжение себя от себя.” [11,77]

В качестве примера такого сверхрассудочного синтеза философ приводил построение иррациональных чисел.  

Стоит отметить, что понятие иррационального числа в том виде, в котором использует его современная математика, сформировалось относительно недавно – в 70-х годах 19 века в работах Вейерштрасса, Гейне, Кантора и Дедекинда. До этого они были, выражаясь словами Павла Флоренского, “туманной нелепостью, которою все бессознательно пользовались ради практической необходимости и в которой не отдавали себе отчета”[11,397], несмотря на то, что человечество столкнулось с ними еще в античности. Во времена пифагорейцев считалось, что существует единая единица длины, достаточно малая и неделимая, которая целое число раз входит в любой отрезок. Однако Гиппас из Метапонта обосновал, что не существует единой единицы длины, поскольку предположение о её существовании приводит к противоречию. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным.

Существует легенда, согласно которой пифагорейцы сбросили Гиппаса за борт корабля как еретика, узнав об этом открытии.

Мы поймем, что такой случай действительно мог произойти, если внимательно рассмотрим учение пифагорейцев. Согласно ему натуральные числа являлись живыми принципами бытия, божественными сущностями из которых был создан космос. Такое отношение могло проистекать из диалектики предельного и беспредельного. Это учение имеет глубокие корни в греческой мысли, можно взять к примеру диалог “Тимей” Платона[13].

Там описывается создание мира из единого беспредельного начала посредством деления, принципами этого разделения являлись числа. Таким образом, числа существуют прежде каждой вещи, являясь мостом между творцом и творением.

Греческий космос, подчиненный натуральным числам, был удивительно гармоничен – планеты в нем вращались в соответствии с изначально заложенной гармонией, кругообороты человеческой души были сопряжены с кругооборотами планет.  Состояние человеческого организма определялось пропорциями четырех элементов –огня, воздуха, воды и земли. Все мироздание можно было свести к изначальной четверке – тетракрису {1,2,3,4}, являвшемуся предметом религиозного почитания. Мир подчинялся числам и их отношением.

Открытие иррациональностей являлось согласно Шпенглеру настоящей диверсией против античного космоса. [14] Несоизмеримость гипотенузы и катета, радиуса и окружности, являлись весточками хаоса – посланниками из чего-то противоположного организованному космосу, поэтому  греки назвали подобные несоизмеримости алогос.

Числа согласно Шпенглеру являлись выражением телесности, а античность была насквозь телесной, поэтому символом ее души “апполоновой” он выбрал статую.

Полной противоположностью апполоновской греческой душе является душа фаустовская – христианская.

Деление, предложенное немецким культурологом, может показаться несколько условным, т.к. изменения происходили непрерывно и порой трудно четко определить принадлежность элемента культуры к той или иной “душе”, например в платонизме немало “фаустовских” моментов. Шпенглеровское разделение следует понимать скорее как некую идеализацию, разведению всего культурного многообразия в соответствии с обозначенными полюсами[1].

И если греческий полюс является телесность, то полюсом христианской души является дух, невидимость, трансцендентность (наиболее ярко это стремление выражено в готическом соборе).

Движущей силой фаустовской души является тоска по абсолюту. Гармония утеряна, появляется представление о чем-то вне мира, способном вернуть ее. Гностики, стоявшие на границе двух культур, фактически вывернули наизнанку греческие представления,  организованный в соответствии с идеей блага  греческий космос становится тюрьмой для духа созданной демиургом. [6]

Новая “душа” создает новую математику, акцент смещается с видимого в невидимое, на смену осязаемой геометрии эвклида и чисел как выразителей вселенских  пропорций  приходят, “невидимые” функции, После Декарта само пространство превращается во множество числовых отношений,  трансцендентных для греческого духа.

    Наиболее яркое выражение фаустовская математика нашла в Лейбнице, его предел является символом, аналогичным готическому собору. То, что во времена Зенона являлось неразрешимым, преодолевается христианским математиком в неудержимом стремлении к бесконечному.

Апофеозом развития фаустовской души явилось создание множества иррациональных чисел, которое можно сравнить с обобщенным решением квадратуры круга.

В традиционных культурах круг часто являлся совершенной фигурой, символизирующей небо, время, космический закон, в то время как квадрат связывался с землей, являлся его первым неизменным определением – фиксированным законом.  Эта пара является неизмеримой, число пи связывающее их является “анлогосом”, недоступным рассудку. В этом непостижимая разница между божественным существованием в себе и в мире,  проявившаяся, к примеру, в символике православного или индуистского храма. [3] Однако христианская душа стремится пройти этот водораздел…

4. Потенциальная и актуальная бесконечность.

От земли к небу

При создании иррациональных чисел происходит переход от потенциальной (т.н. “дурной”) бесконечности к актуальной.

Этот переход, пожалуй, является главным подвигом христианского духа. У язычников господствовало понятия о бесконечности как о возможности продолжать какой-либо процесс без остановки.

“Вообще говоря, бесконечное существует таким образом, что всегда берется иное и иное, а взятое всегда бывает конечным, но всегда разным и разным. Так что бесконечное не следует брать как определенный предмет, например как человека или дом, а в том смысле, как говорится о дне или состязании, бытие которых не есть какая-либо сущность, а всегда находится в возникновении и уничтожении, и хотя оно конечно, но всегда разное и разное”  – так говорил Аристотель о бесконечности. [1]

Таким образом, для античности бесконечность представлялась как нечто смутное, безобразное, скорее несуществующее, чем существующее.

С таким представлением Павел Флоренский связывает наиболее печальные стороны языческой мифологии:  “кому как не язычникам знать о призрачности загробного существования и о дурной бесконечности геенских мучений”.[11,209]

Миф о Сизифе, об Окне с ослом непрестанно пожирающем веревку – плод  его непрерывающегося труда, прикованном к скале Прометее – непрестанно терзаемом коршунами - бесконечность древних печальна, тревожна, похожа на смутное воспоминание о чем-то утерянном, это ощущение в конце концов выливается во вселенскую тоску гностиков.

Христиане принесли в мир другую бесконечность – актуальную бесконечность творца, несоизмеримого с тварью Бога, бесконечность спасения. Это новое представление, поначалу полуинтуитивное, символическое, по мере распространения христианства становится основной парагдигмой европейского человечества. Актуальная бесконечность становиться предметом схоластического дискурса,  так еще Фома Аквинский отрицал возможность актуальной бесконечности:

1). Актуально бесконечного множества быть не может, поскольку всякое множество должно содержаться в каком-либо виде множеств. Но виды множеств соответствуют видам чисел, а ни один вид чисел не может быть бесконечным, поскольку всякое число есть множество, измеренное единицей [буквально: одним]. Следовательно, актуально бесконечное множество существовать не может, как само по себе, так и по совпадению.

2). Кроме того, всякое существующее в природе множество сотворено; всякая же сотворенная вещь понимается как одно из проявлений какого-то намерения Творца, ибо Создатель ничего не делает бесцельно. Следовательно, необходимо, чтобы всякая созданная вещь понималась как число. Поэтому существование актуально бесконечного множества невозможно даже “по совпадению”[8, С. 416]. 

 И  “ни один вид чисел не может быть бесконечным”[8,].  Таким образом, у Фомы Аквинского мы находим представление  о числе сходное с Аристотелевским.

 Однако наряду с господствующим схоластическим богословием, главными источниками которого являлись библейское откровение и аристотелевская логика,   наивысшей точки достигшим в философии Фомы, в христианстве присутствовало другое течение – мистическое, отталкивающееся от  новозаветной вести – “царство божие внутри нас”.

Истоки этого мировоззрения можно найти в гностицизме, неоплатонизме, философии Дионисия Ареопагита, и его суть состояла во внутреннем поиске Бога.

“В каждом человеке есть отпечаток Бога” – говорил Мейстер Экхарт.

Философия ученого незнания Николая Кузанского явилось своего рода браком между двумя течениями, в ней мистическое чувство сочетается с изощренной схоластической логикой.  Главным способом познания божества у Николая является отрицание рамок, присущих конечному – тварному миру, эту философию поэтому еще называют отрицательной теологией.

Таким образом, божество свободно от любых модусов, ограничивающих чувственный мир – таким путем он приходит к понятию максимума – удивительной сущности лежащей по ту сторону всех противоречий, являющимся одновременно максимальным отрезком, треугольником, окружностью, радиусом этой же окружности, шаром и т.п.

Максимум Кузанского является актуальной бесконечностью, получившей собственное бытие. Характерно, что этот максимум, как доказывает Николай, является единственным. Это отличает его от канторовской иерархии бесконечностей, предполагающей бесконечное увеличение мощностей.

Борьба между актуальной и потенциальной бесконечностью пронизывает всю последующую христианскую мысль – от лейбницевских монад и бесконечно малых, до кантовских антиномий, это философское и метафизическое противоборство достигло пика в математической мысли 19 века.

Процесс арифметизации пространства, отхода от созерцания к невидимым числовым соотношениям, описанный Шпенглером, начавшийся с Декартовой системы координат, продолженный дифференциально-интегральным исчислением, рассматривавшим геометрию бесконечно малых,  окончательно оформился в арифметических теориях действительных чисел Вейерштрасса и Дедекинда. Кантор завершает этот виток развития программой сведения всей математики к теоретико-множественным конструкциям. Однако на этом пути он сталкивается с рядом казалось бы непреодолимых противоречий.

Для того, чтобы понять их суть, обратимся к известной теореме Кантора о континууме:

Теорема. Множество всех подмножеств счетного множества несчетно.

Доказательство:

Предположим, что существует множество A, равномощное множеству всех своих подмножеств 2^A, то есть что есть биекция f, ставящая в соответствие каждому элементу множества A некоторое подмножество множества A. Рассмотрим множество   f биективно, а , поэтому существует  такой, что f(y) = B. Теперь посмотрим, может ли y принадлежать B. Если , то  , а тогда, по определению B,. И наоборот, если    , то , а следовательно, . В любом случае, получаем противоречие. Следовательно, исходное предположение ложно и A не равномощно 2^A.Теорема доказана.

Заметим, что 2^A содержит подмножество, равномощное A (например, множество всех одноэлементных подмножеств A), а тогда из только что доказанного следует | 2^A | > | A |

В процессе доказательства используется конструкция, напоминающая известные парадоксы Бертрана Рассела,  однако в отличие от последних, представляющих замкнутые антиномические круги, круг Кантора каким-то таинственным образом разрывается.

Здесь можно опять обратиться к Павлу Флоренскому. Согласно ему схема () применяемая в доказательстве от противного является недостаточной, если не доказана обратная возможность ().

Проверим вторую возможность. Теперь нам нужно из  предположения о том, что множество всех подмножеств несчетно вывести обратное утверждение.

Доказательство проведем так, как рассуждал бы математик до появления Канторовской конструкции, основанное на использовании очевидной для него аксиомы  P: Любое бесконечное множество счетно, что являлось очевидным, до предположения о существовании бесконечных множеств разной мощности.

Множество всех подмножеств счетного множества A –счетно.

Доказательство.

Пусть множество всех подмножеств счетного множества A - 2^A  несчетно, следовательно оно конечно но множество  содержит 2^A  бесконечное множество А(т.к. каждый элемент A также является его подмножеством) таким образом мы пришли к противоречию, и следовательно множество 2^A  -счетное. Теорема доказана.

Как мы видим, все зависит только от канторовской предпосылки о существовании множеств мощности более чем счетной, до этого разум натыкался на неразрешимое противоречие.

 Таким образом, Кантором совершается скачок, о котором Флоренский говорил следующее:

“Мы могли бы не вносить его ограничившись теми сущностями, которые нам даны –“т.е. сущностями “конечными” – предавшись позитивистскому обесположению разума и успокоившись на невозможности выйти за границы данных символов. Мы могли также подняться и ввысь – для этого требовалось напряжение воли и подвиг разума –совершенно специфическое усилие и смирение перед объектом исследования понадобилось для создания символов иррациональностей. Создание новой сущности требует свободного подвига. Свобода его выражается в том, что нам дана возможность либо оставаться при “хорошем” старом, либо подняться к “лучшему” новому. Подвиг же – в том, что естественные силы –присущие уму инертность и самодовольство толкают его к коснению в старом, в конечном, “известном”. Нужно преодолеть самодовольство рассудка, порвать магический круг его конечных понятий и выступить в новую среду – в среду сверхконечного, рассудку недоступному и для него нелепому”[11,400-401].

В приведенном высказывании мы узнаем типично фаустовское стремление к преодолению, сверхрациональному синтезу о котором мы говорили в самом начале.

Для подобной операции не подходит ни кантовское априорное созерцание, ни эмпирика, его источник следует искать в чем-то ином…

Для Флоренского он находится в церковном догмате, примечательно, что Кантор также являлся глубоко религиозным человеком.

5. Мнимости в геометрии: зазеркалье

Для того, чтобы понять отличие в мировоззрении Кантора и Флоренского обратимся теперь к собственному математическому творчеству русского мыслителя.

Наиболее значимой его работой, посвященной математике, является “О мнимостях в геометрии”, изданная в 1922 году. В ней он отказывается от традиционной гауссовской интерпретации комплексных чисел и предлагает свою, довольно оригинальную.

Ведь плоскость Кюна-Весселя-Арганда-Гаусса-Коши, используемая в классическом комплексном анализе - “это есть не более как интерпретация, символически являющая, но не исчерпывающая соответственных арифметических сущностей. Плоскость комплексного переменного н е есть еще самое переменное, -- а лишь одно из истолкований такового на языке пространственных образов, и, следовательно, разделяющее с прочими истолкованиями присущие таковым формальные свойства. Ведь, всякое истолкование подлежит тому, что сказано Г.Герцем картинах мира: это есть система образов, взятых произвольно, но соответствующих системе истолковываемой, и притом так, чтобы возможно большее число следствий из принятых истолковывающих образов соответствовало последствиям системы истолковываемой. Мы заранее знаем, что ни при одном способе толкования такой параллелизм следствий не может идти беспредельно далеко”[10, 8].

В традиционной интерпретации комплексные числа изображаются точками декартовой плоскости, координатами которой являются мнимая и действительная часть, отложенные по осям координат.

Главным недостатком подобного построения является невозможность выразить функциональные отношения.  Вся комплексная плоскость отдана под независимые переменные, таким образом, для того чтобы показать комплексные функции, необходимо обратиться к дополнительной плоскости, никак не связанной с первой.

“И потому, хотя мы и утверждаем, что будто точки на этой второй плоскости изображают зависимое переменное, однако, именно только утверждаем, но ничуть не показываем и не доказываем, ибо то, что одно только и могло бы геометрически показать и доказать эту зависимость, - самая связь двух переменных, - остается никак не представленной геометрически и, в порядке геометрическом, т.е. в порядке самой интерпретации, есть голословное утверждение, лежащее вне возможности проверки, т.е. геометрически не существует”[10,33].

 Флоренский  говорит о том, что наряду с чисто формальной интерпретацией мнимости должна существовать такая, которая выражала бы сущность этой идеи. Наряду с  аналитической геометрией, считает он, должен существовать геометрический анализ,  в котором бы закономерности рассудка отражались в закономерностях созерцания.

В качестве альтернативы классической комплексной плоскости и сфере Неймана, ученый предлагает плоскость двустороннюю – в которой на одной стороне “обитают” положительные площади и действительные числа, на другой отрицательные площади и мнимые числа, а в бесконечно малом промежутке между  – ними комплексные числа.

Эта модель оставляет возможность изображать  зависимость между числами – плоскость таким образом становится средой обитания кривых, принимающих действительные, мнимые и комплексные значения, которые проходят через бесконечно-малую толщину словно  “подземные реки”.

В данной работе нас интересуют, прежде всего, не обоснования и аналитические  выводы из этого построения, а предполагаемый архетип, послуживший источником конструирования. В связи с этим для нас также не играет первичной роли  научная  значимость работы, в сравнении к примеру с тем же Кантором. Нас интересует проблема математического творчества и взаимодействие ее с архетипом.

Примечательно, что Флоренский не оставлял за своей теорией сугубо математического значения, проецируя ее на самые “отдаленные” рубежи физики и метафизики.

Так, в 9 главе мнимостей дописанной им в 1922 и приуроченной к … юбилею Данте, философ рассуждает об “изнанке” теории относительности:

“Что собственно значит предельность величины 3 • 10¹⁰ см/сек ? Это значит вовсе не невозможность скоростей равных и больших с, а — лишь появление вместе с ними вполне новых, пока нами наглядно непредставимых, если угодно — трансцендентных нашему земному, кантовскому опыту, условий жизни; но это вовсе не значит, чтобы таковые условия были немыслимы, а может быть, с расширением области опыта, — и представимыми”.

“на границе Земли и Неба длина всякого тела делается равной нулю, масса бесконечна, а время его, со стороны наблюдаемое — бесконечным. Иначе говоря, тело утрачивает свою протяженность, переходит в вечность и приобретает абсолютную устойчивость. Разве это не есть пересказ в физических терминах — признаков идеи, по Платону — бестельных, непротяженных, неизменяемых, вечных сущностей? Разве это не аристотелевские чистые формы? или, наконец, разве это не воинство небесное, — созерцаемое с Земли как звезды, но земным свойствам чуждое?”[10,49]

За пределами скорости света, считает Флоренский, располагаются волшебные края – миры, похожие на кэрроловские – где время течет в обратном направлении, следствие предшествует причине.

Но самое удивительное, что для того, чтобы исследовать эти миры не следует изобретать сверхсветовые аппараты, что и невозможно у Флоренского, также как и у Эйнштейна. Но последний забыл о еще одном источнике – человеческом духе, который и является источником “мнимой физики”. Различие между двумя подходами кроется в различных мировоззренческих основаниях мыслителей. Эйнштейн в своих построениях отталкивался от картезианской метафизики, возможно имеющей корни в иудейском креационизме. Суть того и другого – это наличие непреодолимой пропасти между творцом и тварью, духом и материей, познающим и познаваемым. Отсюда печаль, роднящая иудейскую теологию, кантовскую “Критику чистого разума” и теорию относительности.

Флоренский был близок к  неоплатоникам, для которых не существовало не снимаемой оппозиций между духом и телом, и одно являлось эманацией другого. В этой философии существовала непрерывная иерархия – единое, ум, душа- каждый из этапов проявления был причастен высшему, что давало возможность восхождения по этой лестнице.  Это мировоззрение нашло свое продолжение в  герметизме, теургии, юнговской психологии, некоторых ответвлениях квантовой физики и, конечно же, в православном  мистицизме, представителем которого являлся Флоренский.

Для него чувственное и сверхчувственное были неразрывно связаны:

“в моем мировоззрении физического как такового, т.е. вне его пронизанности духовными и оккультными энергиями, вовсе не существует, и я полагаю, что не магическое надо объяснять физическими причинами, но напротив, так называемое или кажущееся профанам физическим подлежит объяснению через магические силы.”[12,гл 6]

Именно такой двойственной реальностью, он считал,  к примеру, слово, являющее смыслом с одной стороны, и физическим явлением с другой.

В  работе “Иконостас” философ продолжает эту мысль, рассуждая о парадоксе сна, состоящем в том, что иногда внешняя причина, вызвавшая пробуждение, во сне превращается в продолжение длинной цепочки онейрических событий, во времени ощущаемых значительно раньше вызвавшей пробуждение причиной.

Флоренский объясняет это тем, что во сне время течет в обратном направлении.

Одно и то же событие выступает в двух ролях – как часть сонного и как часть действительного сознания.

“Всякий знает, что за краткое, по внешнему измерению со стороны, время можно пережить во сне часы, месяцы, даже годы, а при некоторых особых обстоятельствах — века и тысячелетия. В этом смысле никто не сомневается, что спящий, замыкаясь от внешнего видимого мира и переходя сознанием в другую систему, и меру времени приобретает новую, в силу чего его время, сравнительно со временем покинутой им системы, протекает с неимоверной быстротой. Но если всякий согласен, и не зная принципа относительности, что в различных системах, по крайней мере применительно к рассматриваемому случаю, течет свое время, со своею скоростью и со своею мерою, то не всякий, пожалуй даже немногие, задумывался над возможностью времени течь с бесконечной быстротой и даже, выворачиваясь через себя самого, по переходе через бесконечную скорость, получать обратный смысл своего течения. А между тем, время действительно может быть мгновенным и обращенным, от будущего к прошедшему, от следствий к причинам, телеологическим, и это бывает именно тогда, когда наша жизнь от видимого переходит в невидимое, от действительного — в мнимое. ”[9,6-7]

О чем бы не думал философ, почти всегда его сопровождает идея зеркальности, скрытой изнанки бытия. Эта повторяемость, а также определенная зачарованность, сопровождающая появление образа, наталкивает на предположение о его архетипической природе. Пользуясь методом Шпенглера его можно принять за символ,  указывающий на принадлежность к определенной “культурной душе”.

Символ зеркала встречается почти во всех культурах и обычно играет роль связывающего звена между поту и посюсторонним. Часто человек сравнивается с зеркалом Бога…, но иногда случается и наоборот, подобный взгляд свойственен мистикам. Так Мейстер Экхарт писал: «Душа созерцает себя в зеркале Божества. Бог Сам является зеркалом, которое он скрывает от того, кого Он будет и открывает тому, кому он будет. Чем больше душа способна превысить все слова, тем более она приближается к зеркалу. В этом зеркале имеет место быть единство как чистое нераздельное подобие»[17].

У исламского мистика ибн Араби мы находим похожую метафору:

«Человек, к которому Сущность Бога представляется сама, чтобы быть познанной, не видит Бога; он только видит свои собственные формы в зеркале Бога. Невозможно познать Самого Бога, хотя можно познать, что только в Нем может быть замечена собственная форма».

«Этот процесс, таким образом, имеет место во взгляде в зеркало. Когда ты смотришь в зеркало, ты замечаешь в зеркале себя, ты видишь не само зеркало, хотя все-таки знаешь, что ты видишь свою собственную форму только благодаря зеркалу. Бог Сам по себе обеспечивает этот феномен как лучший символ Его Само-откровения, так что тот, кто получает это откровение, может узнать, что не может увидеть Бога. Попробуй сам - когда ты смотришь на отражение в зеркало, ты не можешь увидеть само зеркало, ты никогда его не увидишь. Это настолько истинно, что некоторые люди, наблюдая этот закон отражения в (физическом и духовном) зеркале, заявляли, что отраженная форма находится между зеркалом и наблюдателем. Это, конечно же, не так; в реальности, это так, как мы уже говорили (а именно, что отраженная форма, поскольку она не находится между нами и зеркалом, не прячет себя от нас, однако это только благодаря зеркалу мы можем видеть форму, отраженную в нем)... [17]

Таким образом, зеркало является символом Бога, только через него человек может видеть формы, однако самого зеркала никогда не видит[2].

Феномен зеркала волновал не только древних, так, по мнению Флоренского он повлиял на Канта: “Огромную заслугою  Канта было указание, что могут быть объекты ничем не различающиеся между собой в понятии, для рассудка, но тем не менее различные, - так что разница постигается между ними лишь при наглядном сравнении. Такими объектами оказываются, например, правая  и левая рука, или правая и левая перчатка, симметричные относительно и равные между собой сферические треугольники и т.п. Правда Кант из этого факта сперва сделал вывод, что пространство – не понятие, а реальность, независимая от рассудка, а потом – что пространство не понятие – а форма созерцания”.[11,486-487]

Таким образом, при переходе через зеркало происходит как бы разрыв рассудка, что сближает его с символикой числа пи, как перехода между небом и землей, о которой мы говорили выше.

Все это проливает свет на стремленье Флоренского заглянуть в промежуток между двумя гранями – как в случае с логическими антиномиями, так и в случае с комплексными числами, расположенными между действительной и мнимой сторонами плоскости.

Именно этот нетипичный случай, случай безразмерности, граница бесконечной массы и бесконечного времени в теории относительности, становится  средой, в которой путешествует причудливая мысль православного ученого, и именно это чувство постоянной связанности тварного и божественного отличает его от Кантора, типично фаустовского мыслителя, стремящегося к абсолютно трансцендентному Богу.

Это различие между православным и западно-церковным мышлением прекрасно выразил Сергей Булгаков, говоря о церковном обычае освещать природу:

“Общий смысл и основание всех этих освящений тот, что в них уже предваряется(а вместе приуготовляется) новая тварь, преображение твари, “ новое небо и новая земля”. Спиритуалистический рационализм в протестантизме сего легче видит в этом “магизм” или языческое суеверие, умаляя и ограничивая силу христианства одним духовным миром человека. Но человек есть воплощенный дух, существо космическое, в нем живет и с ним освещается и космос, ибо Господь есть спаситель не только души, но и тела, а с ним и всего мира” [2, 258]

Поэтому у Флоренского мы видим зеркало – как символ парадоксальной грани мнимого и действительного, где познавать и быть познаваемым одно и то же, в котором Бог отражает человека, а человек Бога, а у Кантора – похожую на ветхозаветную лестницу Якоба, иерархию бесконечностей,  устремленную в беспредельность, без всякой надежды ее достичь.

Стремление Кантора избежать противоречия в построении действительных чисел поднимает его на более высокий уровень, создавая метабесконечность, в конечном счете, упирающуюся в парадокс Рассела о множестве всех множеств, не содержащих самих себя, это “сверхмножество” неизлечимо от самопротиворечивости так же,  как ”максимум” Кузанского или “истина”  Флоренского.

В отличие от западного мыслителя, стремящегося избежать противоречия (“жертвы рассудка”) любой ценой, отодвигая тем сам абсолютное на  некую недостигаемую высоту, Флоренский утверждает антиномию – как основание всего познания. Это позволяет ему свести “горнее” и  “дольнее”,  помещая Бога между любыми прекословиями бытия. Тем самым Бог оказывается значительно ближе, находясь между внешним и внутренним в каждой вещи, но оставаясь при этом абсолютно, непостижимым, принадлежащим “нигде-стране”, он находится одновременно “в” и “вне” мира, что позволяет приближаться к нему посредством символа, взятого из мира чувств, при этом признавая за ним сверхчувственное существование.

 Мы видим, что наряду с готическим стремлением прорваться к Богу любой ценой, у Флоренского присутствует и абсолютно другое чувство, для которого, пожалуй, подходит придуманный Шпенглером термин арабской, “магической души”. Это подтверждается упомянутым нами сходством с некоторыми исламскими религиозными мыслителями и,   вполне логично, если учесть византийское происхождение русской церкви, и географически и культурологически указывает на пересечение двух культур.

Возможно, этой  раздвоенностью  объясняется два противоположных стремления ученого: проникнуть в “зеркало” и проникнуть “за зеркало”. Из второго стремления, спроецированного на эйнштейновскую физику, вытекает другой архетип – бегущее назад время, поворот  вспять вод Иордана, миф о золотом веке, утерянном райском блаженстве и т.п.

Павла Флоренского можно назвать традиционалистом, эстетом антисовременности, что хорошо подтверждается последней главой “Мнимостей”, защищающей докоперниковскую аристотеле-птоломеевскую модель солнечной системы с центром на земле.

Для мыслителя две стороны зеркала неравнозначны, здесь уместно вспомнить сказку любимого им логика Льюиса Кэрролла “Алиса в зазеркалье”, где девочка с удивлением обнаруживает по ту сторону стекла, абсолютно другую, подчиненную причудливым законам  страну.

Если углубляться в этимологию слова «мнимость» (мнение) можно сравнить его с санскристким manas (разум, человек), литовским menù (вспоминать) или английскими main (разум, память, душа) и man (мужчина, человек).  Таким образом, “мнимая геометрия”, “мнимая физика” – это физика души, предметы, интересующие священника больше чем “действительные” сестры этих наук.

В то же время слово мнимый имеет в разговорном языке скорее негативный оттенок, обозначая что-то ненастоящее, несуществующее, ложное. В таком значении слово также часто употребляется Павлом Флоренским:

“Отныне навеки самость - мнимо-существующая,  само-сознающая идея самоутверждающегося греха и муки.“[11,206]

С этим связана библейская символика зерен и плевел, обоюдоострого меча и т.п. Речь идет о глубочайшей тайне христианства – отделения добра и зла.

Несмотря на кажущееся противоречие двух значений слова “ мнимый” они вполне уживаются в рамках христианской догмы.

Как мы уже показали чуть выше, оно ведет родословную от  санскритского manas означающего одновременно человека и разум. Это отождествление в древних культурах являлось широко распространенным (возьмем хотя бы русское чело и век – вечный разум).

Таким образом, «мнимый» может быть понято как человеческий в противоположность божественному – отсюда два пути, как следствие дарованной твари свободы.

Именно через эту “серединную” человеческую природу, любая вещь может вернуться к Богу – считал Николай Кузанский. Этому как нельзя лучше соответствует образ течения вспять, возвращения к истоку. Но из нее же ведет начало всяческий грех, отсюда возможность связать плоскость Флоренского не только с зеркалом, но и с обоюдоострым мечом, отделяющим “зерна от плевел”.

Мир мнимостей – это мир промежуточный между божественным и тварным, мир похожий на состояние “тайджасы” в ведах, соответствующему сну – переходному состоянию между пракрити и пурушей, материей и духом. Это “царство целей”,  в противоположность царству причин. Именно здесь происходит выбор и отсюда проистекает ответственность.(см. две дороги по которым расходятся грешники у Данте, Геракл на распутье, камень в русских сказках).

Учитывая это мы можем понять повышенный интерес П.Ф. к мнимостям и определенную ассиметрию между двумя сторонами зеркала.

6. Точка перехода. И еще раз проблема континуума

В последней главе мнимостей, написанной значительно позже основной части и являющейся скорее эстетическим обобщением работы П.Ф.  интерпретирует космологию средневекового поэта Данте с помощью современных ему математических конструкций.

Разбор он начинает со следующего отрывка:

По клочьям шерсти (Люцифера) и коре льдяной,
Как с лестницы, спускалась тень Вергилья.
Когда же мы достигли точки той,
Где толща чресл вращает бедр громаду, —
Вождь опрокинулся туда главой
Где он стоял ногами, и по гаду
За шерсть цепляясь, стал всходить в жерло:
Я думал, вновь он возвращался к Аду.
«Держись, мой сын!» — сказал он, тяжело
Переводя свой дух от утомленья:
«Вот путь, которым мы покинем зло».
Тут в щель скалы пролез он, на каменья
Меня ссадил у бездны и в виду
Стал предо мною, полн благоговенья.
Я поднял взор и думал, что найду,
Как прежде Диса; но увидел ноги,
Стопами вверх поднятыми во льду.
Как изумился я тогда в тревоге,
Пусть судит чернь, которая не зрит,
Какую грань я миновал в дороге.[10,45-46]

Миновав все круги ада, поэты переворачиваются вверх ногами, и продолжают свой путь. Пройдя через чистилище и эмпирей, взглянув оттуда на Славу Божию, Данте оказывается во Флоренции без особого возвращения назад.

Подробно анализируя текст “Божественной комедии”, мыслитель приходит к выводу, что пространство, по которому путешествовал Данте, является односторонней Римановой поверхностью. Это открытие по его мнению бросает “неожиданный пучок света на представление древних о конечности мира”. 

Далее философ говорит о недавно сформулированной теории относительности, которая имеет дело  с похожей идеей пространства.

Пространственно-временные модели Флоренского изучены достаточно хорошо, далее мы остановимся лишь на одном моменте – загадочной точке перехода, между действительным и мнимым, между физическим миром, и миром сверхсветовых скоростей, между сном и явью, точке которую символически можно обозначить местом переворота Дантовских героев,   в которой тело выворачивается через себя:

“мы наглядно представляем себе, как, стянувшись до нуля, тело проваливается сквозь поверхность — носительницу соответственной координаты, и выворачивается через самого себя, — почему приобретает мнимые характеристики.”[10,48]

Идея переворота совершаемого на духовном пути также является архетипической, можно вспомнить, например, германского Одина, провисевшего вниз головой 9 дней на мировом древе Иггдрасиль. Однако нас далее будет интересовать другой вопрос: какова природа этой точки – является ли она протяженной или безразмерной,  мнимой или действительной.

Мнимо-комплексные функции Флоренского хоть и являются плоскими, “все же обладают некоторой толщиной”[10,31] они как бы ныряют с действительной стороны во мнимую, и выныривают с мнимой в действительную,  поэтому он сравнивает их с подземными реками. (Интересно, что подземные реки часто играли роль символов перехода –см. к примеру Стикс у греков.)

Оставляя тем самым за своей плоскостью и ее объектами некую высоту, философ ссылается на Буссинеска, говорящего о дифференциале следующее:

“Дифференциал не обозначает вполне или как говорят, объективно малой разности; он обозначает ее только субъективно, т.е. по нашему понятию обозначает ее напряжением, с которым мы заставляем ее стремиться к нулю, и рассматриваем пределы, к которым будут стремиться результаты вычислений.”[10,31-33]

Таким образом, высота комплексной плоскости является  неким “напряжением”, или “актуально бесконечно малой”, как предлагает ее считать П.Ф.

Мыслитель здесь предвосхищает идеи так называемого нестандартного анализа, разработанного в 70-х годах 20 века.

Его появление дало возможность решения одной математической проблемы, ведущей свое начало еще с апорий Зенона.

Суть проблемы в следующем  – каким образом можно составить из безразмерных геометрических точек нечто протяженное – например, отрезок.

Зенон исходил из двух аксиом

А) Сумма бесконечного числа равных протяженных частей является бесконечной.

Б) Сумма бесконечного числа безразмерных величин равна нулю.

Отсюда он выводил свою очередную дилемму: если отрезок линии разделить на бесконечное число равных частей, то они будут либо обладать положительной длиной, и тогда по аксиоме 1 их сумма (то есть отрезок) будет иметь бесконечную длину, либо не обладать и тогда их совокупность имеет нулевую протяженность.

Ключ к решению этой проблемы математики увидели в теории кардинальных чисел Кантора и сопряженной  с ней теорией меры.

Мера является обобщением понятий длины, площади, объема и пр. на множества более общей природы.

Мера всегда неотрицательна, и обладает свойством аддитивности: мера конечного или счетного множества равна сумме мер его частей. Мера точки равна нулю.

Таким образом, мера множества рациональных чисел принадлежащих интервалу (0,1), является нулевой, как счетная сумма мер точек. Мера же самого отрезка (0,1) принимается за единицу. Таким образом, ненулевая мера появляется за счет оставшегося множества иррациональных чисел. Это множество, как мы уже говорили, является несчетным, обладая мощностью континуум. Следовательно, необходимым условием ненулевой меры является более чем счетная мощность.

Однако, как показывает пример так называемой “канторовой пыли” – множества полученного в результате бесконечного числа итераций, состоящих  в отбрасывании средней трети отрезков, полученных из изначального отрезка посредством этих же итераций, обладающей мощностью континуум и нулевой мерой – это условие не является достаточным и дилемма Зенона остается в общем-то нерешенной.

Павел Флоренский писал, что из линейного континуума точек – рациональных и иррациональных- идея протяженности не выводится. Для того, чтобы получить протяженность, нужна “интуиция сплошного”. Таким путем он приходит к идее двойственной точки, содержащей полноту и пустоту.

“Единица и нуль, как значения точки – суть пределы, но можно использовать точку и как стремящегося к этим пределам. Тогда она понимается как дифференциал, причем дифференциал в двояком смысле: либо как “дух возникающей величины”, кирпичик из которого строится величина, тут дифференциал имеет тайную склонность сближаться с актуально бесконечно малым. В этом смысле он некая единица, и не случайно дифференциалы Лейбница были родными братьями его монад, уже знакомых единиц, либо точка получает значение “духа исчезнувшей величины”, точнее исчезающей, и тогда она своего рода нуль: это Ньютоновские флюксии, которые и обозначались кстати у Ньютона точкою, поставленной над буквенным символом соответствующей величины.”[10,31-33]

Таким образом, можно прийти к решению дилеммы Зенона, считает, комментатор “Мнимостей”  Л.Г. Антипенко – заполнив промежутки между действительными числами бесконечно малыми.

Сходные мысли по поводу протяженной точки выдвигал французский философ-традиционалист Рене Генон:

“для наличия такого условия, как протяженность или пространство, необходимы две точки; протяженность (в одном измерении), реализованная, благодаря их одновременному присутствию, в виде расстояния между ними, составляет третий элемент, который выражает отношение между этими двумя точками, одновременно объединяя и разделяя их. Кроме того, это расстояние - если рассматривать его как отношение - явно не состоит из частей; последние были бы лишь другими отношениями расстояния, от которых оно логически независимо”[4,гл “О неопалимой купине”]

приводя дальше онтолого-филологическую интерпретацию:

“Нетрудно понять, что эти три элемента соответствуют элементам высказывания: точки выполняют функцию двух терминов, а промежуток служит выражением отношения между ними, играя роль «связки», т. е. элемента, соединяющего оба термина. Если рассматривать высказывание в его самом обычном и в то же время наиболее общем виде, а именно, как атрибутивное высказывание, в котором в качестве «связки» выступает глагол «быть», то становится понятно, что оно выражает хотя бы относительное тождество субъекта и атрибута. И это соответствует тому факту, что обе точки в реальности представляют собой лишь удвоение одной и той же точки, как бы противостоящей самой себе”.[4,там же]

Подобно этой точке, рассуждает далее Генон, являются едиными в духе познающий, познавание и познание – стоит ли говорить насколько близка идея такого познания русским мистикам.

“Отношение между двумя терминами можно также представить как отношение познания. В этом случае бытие, чтобы познать себя, сопоставляет себя с самим собой, раздваиваясь на субъект и объект, но притом оставаясь единым. Данное утверждение можно распространить на всякое истинное познание, в сущности заключающее в себе отождествление субъекта и объекта, которое сводится к формуле «познающий есть познаваемое». Отсюда ясно, что данная точка зрения напрямую соотносится с предшествующей, ибо можно сказать, что познаваемый объект есть атрибут (или, что то же самое, - модальность) познающего субъекта”[4,там же].

Таким образом, в актуально бесконечно-малой можно в свернутом виде найти ключевые для Павла Флоренского идеи троицы и единства познающего и познаваемого. Учитывая приведенные выше соображения о символике зеркала, в этом можно увидеть более, чем простое совпадение.

Также эту точку перехода между действительным и мнимым можно сравнить с двуликим Янусом, являющимся символом перехода между восходящей и нисходящей половиной годового цикла.

На этом мы пока закончим наше исследование.

Заключение

Исходя из предположения о сверхрассудочности математического синтеза, нам удалось сопоставить некоторые математические структуры, возникавшие у Кантора и Флоренского, с некоторыми довольно общими для всего человечества архетипами. Стоит отметить, что мы не считаем, что эти структуры сами являются архетипами. Скорее, в силу стремления к абстрагированию, присущему математике, они содержаться в архетипе, являясь подчас в них смутно осознаваемой идеей, т.е. являясь более универсальными принципами. Можно представить, что архетип, повлиявший на творца, словно проносит  через себя математическую идею в его творчество. Это отношение архетипа и математических образов, можно вывести почти по-кантовски – из необходимости человека так или иначе созерцать  архетип. Поэтому в работе нет стремления подчинить математику мифологии или бессознательному, как могло бы показаться, ее цель более скромная и точная - из предположения об участии случайности в математическом конструировании, попробовать сопоставить культурные предпочтения ученых и создаваемые ими структуры. Для этого нами был сделан общий семиотический анализ трудов философов (прежде всего Павла Флоренского), вплоть до выделения часто употребляемых слов, после чего найденные символы сопоставлялись с общечеловеческим символизмом, и математическими разработками мыслителей. То, что у нас получилось – является гипотезой, развитой из произвольного предположения, поэтому имеет ценность в связи с истинностью или ложностью этого предположения, а проецируя современную математическую логику на философию, это можно назвать исследованием новообразованного культурологического пространства, что открывает широкое поле исследований.

Данная работа требует продолжения и дальнейшей детализации.

Библиографический список

1. Аристотель Сочинения. В 4 т. (Серия «Философское наследие»). М.: Мысль, 1975—1983. Т. 3. / Ред и вступ. ст. И. Д. Рожанского. 1981. 616 стр. 220000 экз.

Физика. / Пер. В. П. Карпова.

2. Булгаков С.  “Православие” Категория:Православие Серия:   Философия. Психология Издательство:   ИЗД-ВО "АСТ" ISBN: 5-17-014905-0

3. Буркхард Т. Сакральное искусство Востока и Запада. Принципы и методы. / Пер. с англ. Н.П.Локман М. Алетейа 1999г.

4. Генон Р “Символизм креста” Издательство: Беловодье, 2008 г. 224 стр. ISBN   978-5-93454-095-2 Тираж: 2000 экз.

5. Иммануил Кант “Критика чистого разума” Издательство: Эксмо, 2009 г. 736 стр. ISBN   5-699-14702-1, 978-5-699-14702-1

6. Йонас Ганс Издательство: Лань, 1998 г.384 стр. ISBN   5-8114-0057-8

7. Лосев А.Ф. “История античной эстетики. Последние века” Издательство: Искусство, 1988 г.416 стр.

8. Георг Кантор “Труды по теории множеств” М.:,Наука, 1985.

9. Павел Флоренский “Иконостас”,Издательство: Азбука-классика, 2009 г.224 стр. ISBN   978-5-9985-0699-4

10. Флоренский П. “Мнимости в геометрии” , изд. “Лазарь”, 1991. ББК 22.151 Ф73

11. Павел Флоренский “Столп и утверждение истины”Издательство: АСТ, 2007 г. 640 стр. ISBN   978-5-17-010897-8, 5-17-010897-4

12. Павел Флоренский “У водоразделов мысли” Издательства: АСТ, АСТ Москва, 2009 г. 352 стр.ISBN   978-5-17-059739-0, 978-5-403-01850-0

13) Платон. Собрание сочинений в 4 томах. Том 3. Часть 1

Издательства: Издательство Олега Абышко, Издательство Санкт-Петербургского университета, 2007 г.752 стр. ISBN   978-5-903525-06-5, 978-5-903525-07-2, 978-5-89740-157-4, 978-5-288-04368-0, 978-5-288-04369-7, 978-5-288-04110-0

14. Освальд Шпенглер Закат Европы. Том 1Серия: Антология мысли

Издательство: Эксмо, 2009 г. 800 стр.ISBN   978-5-699-15818-8

15. Юнг К. Г.

Человек и его символы. Издательства: Серебряные нити, Медков С. Б., 2006 г.352 стр.ISBN   5-902582-08-3

Научные работы:

16) Mundus Imaginalis, or the Imaginary and the Imaginal by Henri Corbin-Ipswich: Golgonooza Press, 1976. (Источник статьи в Интернете: http://hermetic.com/bey/mundus_imaginalis.htm

17) Титус Буркхарт “Символизм зеркала”

Интернет-источник http://www.arcto.ru/modules.php?name=News&file=article&sid=1461

18) Катасонов В.Н. /ЛЕСТНИЦА НА НЕБО

(Генезис теории множеств Г.Кантора и проблема границ науки)(Интернет–источник: http://ru.philosophy.kiev.ua/iphras/library/granitsy/katasonov.htm

19) В.Н. Арнольд “Математическая дуэль вокруг Бурбаки”

(Интернет-источник: http://www.mccme.ru/edu/index.php?ikey=viarn_burbaki