Криптограмма (по-гречески

Криптограмма

Коды появились в глубокой древности в виде криптограмм (по-гречески - тайнопись). Порой священные иудейские тексты шифровались методом замены. Вместо первой буквы алфавита писалась последняя буква, вместо второй - предпоследняя и так далее. Этот древний метод шифрования назывался атбаш. Известно, что шифровалась переписка Юлия Цезаря (100 - 44 гг. до н. э.) с Цицероном (106 - 43 г.г. до н. э.).Шифр Цезаря реализуется заменой каждой буквы в сообщении другой буквой этого же алфавита, отстоящей от нее в алфавите на фиксированное число букв. В своих шифровках Цезарь заменял букву исходного открытого текста буквой, отстоящей от исходной буквы впереди на три позиции.

С начала эпохи Возрождения (конец XIV столетия) начала возрождаться и криптография. Наряду с традиционными применениями криптографии в политике, дипломатии и военном деле появляются и другие задачи - защита интеллектуальной собственности от преследований инквизиции или заимствований злоумышленников. В разработанных шифрах перестановки того времени применяются шифрующие таблицы, которые в сущности задают правила перестановки букв в сообщении.

В качестве ключа в шифрующих таблицах используются: а) размер таблицы; b) слово или фраза, задающие перестановку; c) особенности структуры таблицы.

Одним из самых примитивных табличных шифров перестановки является простая перестановка, для которой ключом служит размер таблицы. Этот метод шифрования сходен с шифром скитала. Например, сообщение

ТЕРМИНАТОР ПРИБЫВАЕТ СЕДЬМОГО В ПОЛНОЧЬ

записывается в таблицу поочередно по столбцам. Результат заполнения таблицы из 5 строк и 7 столбцов показан на рис. 1.После заполнения таблицы текстом сообщения по столбцам для формирования шифртекста считывают содержимое таблицы по строкам.

Т	Н	П	В	Е	Г	Л
Е	А	Р	А	Д	О	Н
Р	Т	И	Е	Ь	В	О
М	О	Б	Т	М	П	Ч
И	Р	Ы	С	О	О	Ь

Рис.1.Заполнение таблицы из 5 строк и 7 столбцов

Если шифртекст записывать группами по пять букв, получается такое шифрованное сообщение:

ТНПВЕ ГЛЕАР АДОНР ТИЕЬВ ОМОБТ МПЧИР ЫСООЬ

Естественно, отправитель и получатель сообщения должны заранее условиться об общем ключе в виде размера таблицы. Следует заметить, что объединение букв шифртекста в 5-буквенные группы не входит в ключ шифра и осуществляется для удобства записи несмыслового текста. При расшифровании действия выполняют в обратном порядке.

Несколько большей стойкостью к раскрытию обладает метод шифрования, называемый одиночной перестановкой по ключу. Этот метод отличается от предыдущего тем, что столбцы таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.

Применим в качестве ключа, например, слово Пеликан а текст сообщения возьмем из предыдущего примера. На рис.2 показаны две таблицы, заполненные текстом сообщения и ключевым словом, при этом левая таблица соответствует заполнению до перестановки, а правая таблица - заполнению после перестановки.

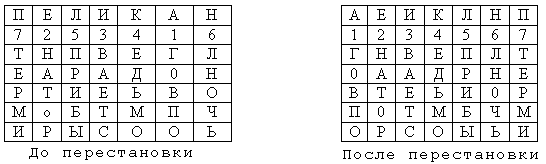
Рис.2.Таблицы, заполненные ключевым словом и текстом сообщения

В верхней строке левой таблицы записан ключ, а номера под буквами ключа определены в соответствии с естественным порядком соответствующих букв ключа в алфавите. Если бы в ключе встретились одинаковые буквы, они бы были понумерованы слева направо. В правой таблице столбцы переставлены в соответствии с упорядоченными номерами букв ключа.

При считывании содержимого правой таблицы по строкам и записи шифртекста группами по пять букв получим шифрованное сообщение:

ГНВЕП ЛТООА ДРНЕВ ТЕЬИО РПОТМ БЧМОР СОЫЬИ

Для обеспечения дополнительной скрытности можно повторно зашифровать сообщение, которое уже прошло шифрование. Такой метод шифрования называется двойной перестановкой. В случае двойной перестановки столбцов и строк таблицы перестановки определяются отдельно для столбцов и отдельно для строк. Сначала в таблицу записывается текст сообщения, а потом поочередно переставляются столбцы, а затем строки. При расшифровании порядок перестановок должен быть обратным.

Пример выполнения шифрования методом двойной перестановки показан на рис. 3. Если считывать шифртекст из правой таблицы построчно блоками по четыре буквы, то получится следующее:

ТЮАЕ ООГМ РЛИП ОЬСВ

Ключом к шифру двойной перестановки служит последовательность номеров столбцов и номеров строк исходной таблицы (в нашем примере последовательности 4132 и 3142 соответственно).

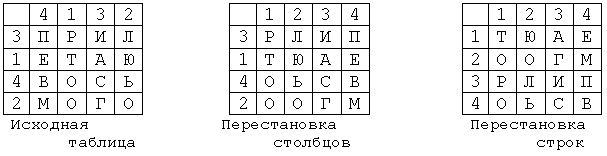
Рис. 3. Пример выполнения шифрования методом двойной перестановки

Число вариантов двойной перестановки быстро возрастает при увеличении размера таблицы:

• для таблицы 3х3 36 вариантов;

• для таблицы 4х4 576 вариантов;

• для таблицы 5х5 14400 вариантов.

Однако двойная перестановка не отличается высокой стойкостью и сравнительно просто "взламывается" при любом размере таблицы шифрования.

Применение магических квадратов

В средние века для шифрования перестановкой применялись и магические квадраты.

Магическими квадратами называют квадратные таблицы с вписанными в их клетки последовательными натуральными числами, начиная от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число.

Шифруемый текст вписывали в магические квадраты в соответствии с нумерацией их клеток. Если затем выписать содержимое такой таблицы по строкам, то получится шифртекст, сформированный благодаря перестановке букв исходного сообщения. В те времена считалось, что созданные с помощью магических квадратов шифртексты охраняет не только ключ, но и магическая сила.

Пример магического квадрата и его заполнения сообщением ПРИЛЕТАЮ ВОСЬМОГО показан на рис. 4.

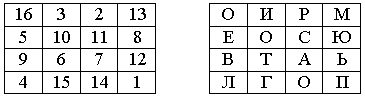
Рис. 4. Пример магического квадрата 4х4 и его заполнения сообщением

ПРИЛЕТАЮ ВОСЬМОГО

Шифртекст, получаемый при считывании содержимого правой таблицы по строкам, имеет вполне загадочный вид:

ОИРМ ЕОСЮ ВТАЬ ЛГОП

Число магических квадратов быстро возрастает с увеличением размера квадрата. Существует только один магический квадрат размером 3х3 (если не учитывать его повороты). Количество магических квадратов 4х4 составляет уже 880, а количество магических квадратов 5х5 - около 250000.